思维训练之红黑树
Contents
《STL源码分析》中关于红黑树(RB-tree)的描述引发的思考:
如何解决一个问题 一般而言,问题域会分解为下面几个方面: a. 期望结果是什么?可以是数据结果或行为结果;包含正常反馈与异常反馈。 b. 哪些基础信息提供?包含静态不变信息、动态信息输入、限定条件、从基础信息到期望结果的流程。 c. 如何规划业务数据?如何在业务数据上执行业务逻辑? a,b方面为业务先决条件,属于面向问题(面向客户)的调研、分析与设计。c方面为业务是否可实现、实现代价、性能评估,属于面向实现(面向开发)的分析与设计。c方面剥离大部分业务概念,可提取出一个或者多个核心抽象模型,模型与业务流程通过组合构成c方面的主干。
核心抽象模型 核心抽象模型此处指的是剥离绝大部分业务细节,提取的最贴近计算机的、贴近数学的数据与算法,可以分为以下几块: a. 原始数据 b. 数据使用限定 c. 结果数据 d. 基于原始数据的数据结构,亦或数据组织形式 e. 基于数据结构的运行规则(包含变换逻辑、限定规则等) f. 基于数据结构与运行规则的算法逻辑 a、b、c项倾向于数据的抽象;d、e、f项即使在a、b、c项完全相同时,考虑到CPU、IO、内存、耗时等性能指标,也可能不同。不妨把d、e、f取一个好听的名字:设计模式。
(由于鄙人不善于记忆,往往以推导或故事的方式,所以文中存在一些假设性的推理,助记忆。)
tree(树)
树是一种常见的结构,往往通过递归的方式定义,非空树由一个根节点以及0个或n个子树构成,有明确的父子兄弟关系。无论是计算机语言,还是分析问题的思路(自顶而下分析法),甚至是日常所见,都充斥了树的思想,如下图所示:
 往往越简单的东西越具有普遍适用性,但其解决问题的能力也相对较弱。对于树,若添加少量约束,可以覆盖其部分频繁使用的场景,并拥有不错的效率,那也是值得研究的。对于树的约束,大可以分为横向约束、纵向约束、数据约束,前两种约束了树的的形状,后一种约束了数据的排布。
往往越简单的东西越具有普遍适用性,但其解决问题的能力也相对较弱。对于树,若添加少量约束,可以覆盖其部分频繁使用的场景,并拥有不错的效率,那也是值得研究的。对于树的约束,大可以分为横向约束、纵向约束、数据约束,前两种约束了树的的形状,后一种约束了数据的排布。
binary tree(二叉树)
二叉树是对于树的横向约束。 对于树,一个节点下可以挂载0->n个子树,那么0->n选取哪个值作为边界最为恰当?
- 0,限制子树小于或等于0无意义,只能构建仅有根节点的树;限制大于0无意义,叶子节点的子树必然为0,非叶子节点的子树必然不为0。维度:点
- 1,限制子树小于或等于1无价值,构建出来的是个列表,使用列表算法更优;限制大于1无意义,同0场景。维度:1维
- 2->n,限制子树小于或等于m,同父节点下,兄弟节点的关系最多有$\frac{m(m-1)}{2}$种情况,即m=2,关系数1;m=3,关系数3;m=4,关系数6…,关系数越多,算法所需要处理的场景越复杂;限制大于m,借鉴子树小于等于的场景,关系数至少为3,复杂度高(即使存在这样的场景,树的算法一般也能满足,树不能满足的场景下,必有额外的业务条件,需要定制算法,通用性不强。当然不排除找到合适的规则和算法后,这具有更高的效率。)。维度:m维
所以综合而言,定义一种树,叫二叉树,约束子树数量不超过2,在树横向约束的基础上进行特化(窃取了模板的概念),拥有适宜的灵活性、场景适应性以及较小的复杂度。(进一步特化,约束子树数量等于2,那便是完全二叉树。再进一步约束每层节点数都达到最大值,那便是满二叉树。)
binary search tree(二叉查找树)
二叉查找树是对于二叉树的数据约束。 二叉树有一个重要的应用,快速查找。要实现查找能力,那么作为二叉树节点的对象之间必须是可比较的,即,有明确的大于、小于与等于关系。节点的数据对象在树上需要按照一定规律进行排布,基于数据对象排布规则的算法可以实现数据对象的快速查找。于是,聪明的人们定义了一套规则,并把基于此规则的二叉树叫二叉查找树。
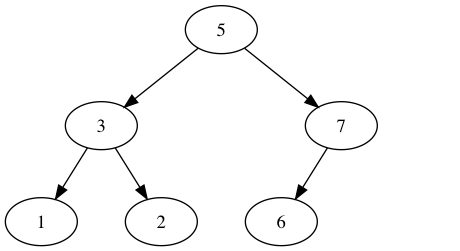
二叉查找树节点放置规则:任何节点的键值一定大于其左子树中每个节点的键值,并小于其右子树中每个节点的键值。
如上定义的二叉查找树便有了以下特征:
- 顺着根节点,一直往左走,直到无左路可走,可获得最小值。
- 顺着根节点,一直往右走,直到无右路可走,可获得最大值。
- 首先遍历左子树,然后访问根节点,最后遍历右子树(中序遍历),可以获取到一个升序队列。
- 二叉查找树的查找时间复杂度介于$O(log^N)$与O(N)之间。
如下为二叉查找树的示例:
ADT之查
| |
从根节点开始往下查找e(参考二叉查找树节点放置规则):
- 空树直接返回NULL;
- 若e比当前节点对象小,向当前节点的左子树发起新一轮查询;
- 若e比当前节点对象大,向当前节点的右子树发起新一轮查询;
- 若e等于当前节点对象,返回当前节点位置;
- 若e未找到匹配的对象(同步骤1,查找的子树为空树),返回NULL。
ADT之增
二叉查找树上插入一个新节点,可以很多选择,例如:
- 将新节点作为根节点,再根据新根节点与左右子树的大小进行调整;
- 将新节点插入任意比新节点左小右大的两节点中间;
- 通过查找,找到一个nil叶子节点(树上每个实节点缺失的左子或右子都视为nil叶子节点,nil叶子节点具有位置信息,但无数据对象),把这个nil叶子节点布置为新节点;
- 等等
这里采用在nil叶子节点布置新节点的方式,粗略来看有以下这些好处:
- ADT之查的算法逻辑可复用,恰似新节点本就该在那个位置,新树必然满足二叉查找树的性质
- 将新节点布置在nil叶子节点,无需考虑插入到非nil节点时左右子树的调整
| |
从根节点开始往下查找可布置e的nil叶子节点:
- 空树直接创建根节点,并返回树;
- 若e比当前节点对象小,向当前节点的左子树发起新一轮查询;
- 若e比当前节点对象大,向当前节点的右子树发起新一轮查询;
- 若e等于当前节点对象,无需新增节点,返回当前节点位置;
- 若e未找到匹配的对象(同步骤1,查找的子树为空树),在查找的最后位置(即nil叶子节点),布置新节点。
ADT之删
删除一个节点,这绝对是个麻烦事儿。增加一个节点时,引导其查找并覆盖一个nil叶子节点,删除却具有不确定性,可以删除叶子节点,也可以删除一个中间节点,甚至删除根节点,着实让人操碎了心。不妨先做以下分析:
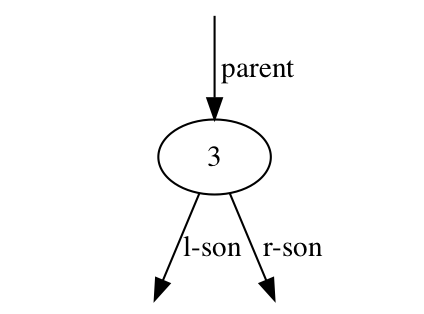
删除一个节点,往往需要考虑三个关系(parent、left-son、right-son)的重整。这三个关系又可以分为两类:必有,parent(根节点往往也会挂在树的某个管理节点下);可有,left-son、right-son(左右子树在地位上无差异)。如此,分析可以得出两种关系调整场景、三种数据结构场景。 关系调整场景:调整parent关系、调整son关系 数据结构场景:删除的节点没子(叶子节点)、删除的节点有一个子(单子节点)、删除的节点有两个子(双子节点)
删除叶子节点:直接删除parent关系,无子无压力,是最为简单的场景。
删除单子节点:直接将单子节点的parent关系重新关联到单子节点的子节点。
删除双子节点:直观来看,很难想出什么好办法,那么不妨先尽量偷懒,再看看转换成已经可以解决的场景。 正常销毁一个节点,需要销毁两部分内容:数据对象与结构节点(想个好名字太难,先以结构节点来表示树结构中的节点,不考虑数据;数据节点也就是本文中所说的节点,其中包含数据对象,即使是nil对象)。既然是销毁,那么数据对象肯定是要被干掉的,或者说删除本质是要干掉数据对象,移除数据对象后的结构节点若破坏了二叉查找树的性质,这才必须处理。那不妨想想办法:
- 不移动结构节点,但该节点必须得满足两个性质:a. 不能被查找或删除;b. 可比较,查找路过此节点时,可正确选择左右孩子。针对a性质,添加个已删除标记即可,针对b性质,保留原数据对象的键值即可。这懒树行为简直将删除的性能提升到了极致,但,树在膨胀。内存占用上,每个节点多了个已删除标记,无效节点依然占据内存;性能上,查找与删除需要路经无效节点,额外的对比与访问开销;算法上,每次均需要识别节点标记。(不适合无重复数据的树,但对允许数据重复的树,倒是个不错的选择)。
- 看做nil节点,把nil数据对象往子树转移,不停的做父子交换,直到单子节点或叶子节点。如此便需要将其中一个子节点上移,每次子树数据对象的上移,子树的左右子树必须重新调整结构。根据每个节点的数据结构场景有3种,左右子树在地位上无差异,那么需要考虑的场景大约有$\frac{({3}\times(3-1))}{2}+3=6$种,其中最复杂的便是双子节点的左右子树都是双子节点。实在是太搞脑子了,先缓缓。
- 看做nil节点,把nil数据对象往子树转移,直接查找子树可交换的单子节点或叶子节点。回想下二叉查找树的性质,用来替换的子节点需要满足比左子树每个节点都大,比右子树每个节点都小,若删除的是左子,要比父节点小,若删除的是右子,要比父节点大,那该删除节点下左子树的最大值与右子树的最小值…不肖多说了。而且这俩节点必然是单子节点或者是叶子节点(反推如果是双子节点,那必然有更大和更小的值)。
| |
从根节点开始往下查找到e,找到e后进行删除与变换:
- 空树找不到要删除的e,直接返回;
- 若e比当前节点对象小,向当前节点的左子树发起新一轮查询;
- 若e比当前节点对象大,向当前节点的右子树发起新一轮查询;
- 若e等于当前节点对象,开始执行删除算法;
- 若是双子节点,找到右子树的最小值替换到当前节点的数据对象,并继续删除右子树最小值;
- 若是单子节点,用唯一的子替换当前节点,并销毁当前节点;
- 若是叶子节点,销毁当前节点
- 若e未找到匹配的对象(同步骤1,查找的子树为空树),直接返回。
ADT遗留问题
二叉查找树已经可以很好的解决问题,但还有个恼人的情况,若向树上增加的数据已经有序(升序为例),那生成的树将会变成如下所示:
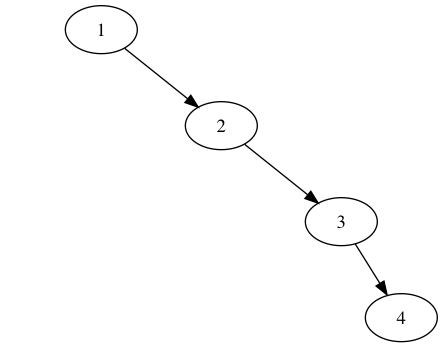
这类极端情况便是二叉查找树查找时间复杂度为O(N)的典型代表,如此一来倒不如使用链表更清爽一些。 为了进一步提升查找性能,自然希望节点分布均匀些,若是每棵树都是完全二叉树,那岂不是美滋滋。但应该如何去衡量节点分布均匀?
- 先想了个试试,不妨添加nil节点,将这棵树构建成一个满二叉树,如下图所示:
 这便是个等边三角形,其高度为h(上图为3),底边长为m(上图为8),$m=2^{h}$,其面积$s=2^0+2^1+…+2^h=2^{h+1}-1$。其中有效节点数为N(上图为4),那其有效利用率为$b=\frac{N}{2^{h+1}-1}$,需得满足条件${2^{h+1}-1}\geq{N}$,即${h}\geq{log^{N+1}-1}$。h越接近最小值,其有效利用率越高,分布相对均匀。如上图所示,h当前值为3,有效利用率$b=\frac{4}{2^4-1}=0.27$,h最小值可取到2,此时有效利用率$b=\frac{4}{2^3-1}=0.57$。
这便是个等边三角形,其高度为h(上图为3),底边长为m(上图为8),$m=2^{h}$,其面积$s=2^0+2^1+…+2^h=2^{h+1}-1$。其中有效节点数为N(上图为4),那其有效利用率为$b=\frac{N}{2^{h+1}-1}$,需得满足条件${2^{h+1}-1}\geq{N}$,即${h}\geq{log^{N+1}-1}$。h越接近最小值,其有效利用率越高,分布相对均匀。如上图所示,h当前值为3,有效利用率$b=\frac{4}{2^4-1}=0.27$,h最小值可取到2,此时有效利用率$b=\frac{4}{2^3-1}=0.57$。 - 再想个试试,还以1中的图为例,假定图中每个节点的深度为从自身往父查找到的第一个非nil节点的深度,提取深度最深的一群节点(包含nil节点),计算标准差$\sigma=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(d_i-\mu)^2}$,其中$\mu=\frac{d_1+d_2+…+d_n}{n}$,$n=2^h$。如上图所示,$h=3$,$n=2^3=8$,$\mu=\frac{0+0+0+0+1+1+2+3}{8}=0.875$,$\sigma\approx1.053$;若$h=2$,$n=2^2=4$,$\mu=\frac{1+1+1+2}{4}=1.25$,$\sigma\approx0.433$。
- 直观来想,每逢一个双子节点的判断,可以剔除一个子树,没逢一个单子节点的判断,不会剔除子树,在节点总数确定的情况下,拥有的双子节点数越多,需要比较的次数越少,查找的性能越高。那再试试以下的公式$b=\frac{当前树的双子节点数}{完全二叉树的双子节点数}$,1中图例$b=\frac{0}{1}=0$,若$h=2$,无论如何排布都存在一个双子节点,$b=\frac{1}{1}=1$。
以上是对于节点分布是否均匀的衡量方式的尝试(有可能定式思维,将所有的指标都往树的高度上靠)。 专业的说法叫平衡,没有任何一个节点深度过大。通过增加一些纵向约束达成,常见的有AVL-tree、RB-tree、AA-tree等。(从完美的角度,完全二叉查找树是个不错的选择,然而根据二八定律,构造一个普遍适用的完全二叉查找树,其难度与代价…)
RB-tree(红黑树)
红黑树是二叉查找树的一种纵向约束。 关于红黑树的历史,就能力所查,它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。这…想要揣摩红黑树的发家历程,看来难度不止一点儿。有个有意思的说法,读着很解气:
注水的艺术 不同于AVL树的一本正经,红黑树走的是猥琐路线。我们不是想要一棵平衡树吗?好,先来一棵完美的平衡树,它从根到叶的所有路径都等长。我们把这棵树称为黑树。但是,黑树实在太完美了,我们很难从它身上捞到什么好处。于是,我们要对黑树进行注水。注进去的点,我们称之为红点,注过水的黑树就成了红黑树。 不过,注水还有些讲究。有点像视频中过渡帧依赖于关键帧,在红黑树中,红点只允许出现在黑点之后。这确保了树中最长路径(半红半黑)的长度不会超过最短路径(全黑)长度的两倍,与AVL树有异曲同工之妙。
RB-tree之约束
- 每个节点不是红色就是黑色
- 根节点为黑色
- 如果节点为红,其子节点必须为黑
- 任一节点至nil节点(树尾端)的任何路径,所含黑节点数必须相同
- 每个nil叶子节点(下图未画出)视为黑色
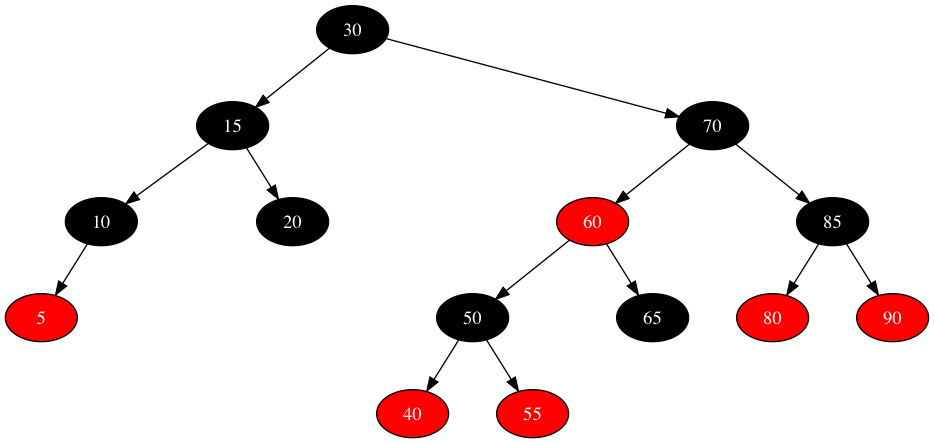
RB-tree从节点结构上可以分为根节点、双子节点、单子节点、叶子节点、nil叶子节点:
- 根节点:除空树外,每棵树都有一个根节点,是增、删、查动作的总入口
- 双子节点:拥有2个子节点的树节点
- 单子节点:拥有1个子节点的树节点,缺失的左子或右子标记为nil叶子节点
- 叶子节点:拥有0个子节点的树节点,缺失的左子和右子标记为nil叶子节点
- nil叶子节点:单子节点和叶子节点缺失的左子或右子标记为nil叶子节点,空树的根节点就是nil叶子节点。(根据实现不同,nil叶子节点可能是其父指向NULL,也可能是数据对象为NULL的叶子节点,上图中未画出)
RB-tree从节点颜色上可以分为红色、黑色(规则1):
- 规则3:加上规则1,限制了从根节点到任意nil叶子节点的$红色节点\leq黑色节点+1(包含nil叶子节点)$
- 规则2:加上规则1、3,限制了从根节点到任意nil叶子节点的$红色节点\leq黑色节点(包含nil叶子节点)$
- 规则5:加上规则1、3、2,限制了从根节点到任意nil叶子节点的$红色节点\leq黑色节点-1(包含nil叶子节点)$,即$红色节点\leq黑色节点(不包含nil叶子节点)$
- 规则4:加上其他规则(以下的黑色节点均指从根节点到任意nil叶子节点路径上黑色节点数,不包含nil叶子节点)
- 从根节点到任意nil叶子节点的节点数(深度或高度+1)应在范围$[黑色节点,2\times黑色节点)$内
- 黑色节点所能支撑的树节点总数N的范围$[2^{黑色节点}-1,2^{2\times黑色节点}-1)$,即黑色节点数的范围为$[\frac{1}{2}log^{N+1},log^{N+1})$
- 若某个节点为黑色,那其父节点到根节点的所有节点必然是双子节点
- 若某个节点为红色,那其必然是双子节点或叶子节点
- 双子节点数至少有$2^{黑色节点-1}-1$个(全黑满二叉树是最少的情况之一)
- 若不存在红色节点,那这棵树必然是满二叉树
红黑树通过给二叉查找树加上颜色维度的限制(回想下**“注水的艺术”**),限制了树的深度,保障了双子节点数。 红与黑的概念还可以通过其他概念进行替换,比如**虚与实**,个人比较喜欢,也比较形象。红黑树上的每个黑色节点看做**实节点**,实节点有重量,每个红色节点看做**虚节点**(virtual),虚节点无重量,用于缓冲实节点与实节点之间的关系,所以两个虚节点之间的联结无意义。何为**平衡**,即像杠杆(秤杆也行)一样,当提起其中任意一个节点作为支点时,其左右子树作为杠杆的两端是平衡的(此处经不起力矩($实节点\times实节点距离支点节点的路径长度$)概念的敲打)。
RB-tree之查
同ADT之查。
RB-tree之增
参考ADT之增,将新节点插入到树尾(亦可理解为替换查找到的nil叶子节点)。 为了满足规则1,需要对新节点着色,在优先保证平衡(规则4)的条件下,新节点标记为红色,此时规则5天然满足,但规则2与规则3依然存在风险。所以对于新增节点的场景,剩下的便是调整树结构,满足规则2与规则3。
- 规则2针对根节点,而根节点只可能作为杠杆的支点,所以根节点颜色是黑还是红,并不影响整棵树的平衡,但还是任性的将根节点标记为黑色(根节点如果为红色会影响平衡时树的结构,具体影响尚未想清晰)。每次根节点由红色变为黑色时,根据黑色节点所能支撑的树节点总数N的范围$[2^{黑色节点}-1,2^{2\times黑色节点}-1)$,可以认为是树的扩容。
- 规则3最麻烦的是新节点与其父都是红色,在这种情况下,需要争取调整红黑的位置(同时必须保持二叉查找树),在保证树平衡的同时,满足此规则。在RB-tree新增节点的场景下,优先找包含新节点与其父的最小子树进行调整,若无法进行调整,说明需要进行最小子树的扩容(即往此子树添加黑色节点,也可理解为黑色节点下沉,红色节点上浮)。从规则2的分析,根节点的扩容是万不得已情况下,唯一的逃生通道,所以当子树无法消化新增的红色节点时,将红色节点上浮,最终可进入逃生通道。
空树场景
插入一个新节点作为根节点,根据规则2,变换根节点为黑色。
###两层最小子树场景
优先考虑最小子树包含两层的场景,如下图所示:
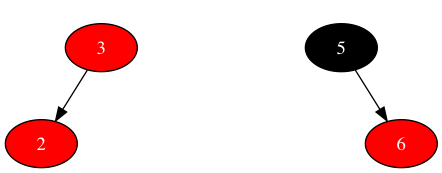
由于树上的红色节点只可能是双子节点或叶子节点,对于左边的场景,新节点之父为红色,那新节点之父必然是叶子节点,此种场景在两层子树中无法通过调整来满足规则3,只能遗留到三层最小子树场景寻找可能性;对于右边的场景,无需调整已满足规则3,即满足所有规则。
三层最小子树场景
对于新节点之父为红色,继续考虑三层最小子树的场景。此时由于新节点之父为红色,其祖父节点必为黑色(规则3),唯一可以求助的便是祖父的另外一条子树,可以分为如下2种场景:
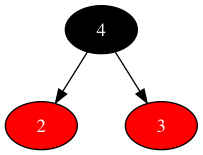
- 场景1:新节点的父为红色,父兄弟为nil叶子节点
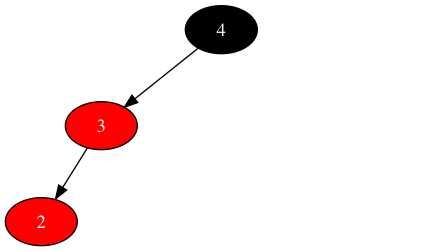
由于红色节点不参与称重(树平衡条件中不包含红色节点),所以在不改变黑色节点在树中位置的情况下,红色节点任意挪动不影响树的平衡。只要将左子树中其中一个红色节点挪到右子树,再调整数据对象的顺序,保持树的平衡即可。即期望中间状态如下:
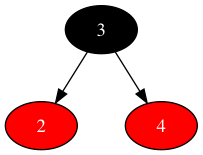
对3、4这两个数据对象重新排序,可以获得最终状态如下:
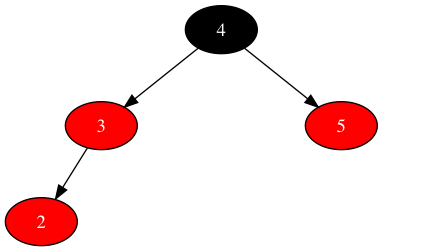
- 场景2:新节点的父为红色,父兄弟为红色
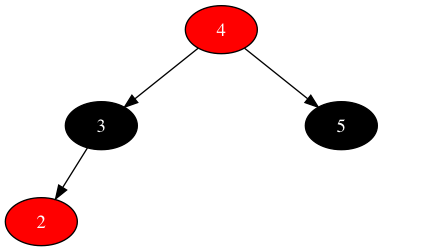
此时该子树无法消化三个红色节点,需要对子树扩容,即黑色节点下沉,红色节点上浮,将问题丢给其祖父去解决,可获得最终状态如下:
场景闭环分析
空树场景、两层最小子树场景、三层最小子树场景,三者已覆盖了RB-tree上新增节点的所有场景,除了三层最小子树场景的场景2,其他场景均彻底解决问题。
三层最小子树场景的场景2,最终状态下,祖父节点就如同新节点一样,面临了一开始所述的问题。如果祖父节点遇到的问题,可以被上述已经分析的场景覆盖,那只需将已调整完的祖父节点当做红色新节点处理即可:
- 空树场景:即场景2中的祖父节点是根节点,变换根节点为黑色,满足所有规则。
- 两层最小子树场景:若祖父节点之父为黑,满足所有规则;若祖父节点之父为红,继续考虑三层最小子树场景。
- 三层最小子树场景:若祖父节点之父为红色,父兄弟为红色,再次进入场景2;若祖父节点之父为红色,父兄弟为黑色,当前仅覆盖了一个子集场景(父为红色,父兄弟为nil叶子节点)。
如上的分析过程,除三层最小子树场景的场景2是个特化场景,其他场景均与已有的分析一致。即完善父为红色,父兄弟为黑色的场景便完成了场景闭环。
三层最小子树场景完善
如下图所示,是父为红色,父兄弟为黑色的场景。其中**B(Brother)**为新节点的兄弟;PB(Parent Brother)为新节点之父的兄弟。由于新节点不再局限于叶子节点(可能是三层最小子树场景之2的祖父节点),下图中的红色节点3便可能是双子节点,那B必然为黑色节点(nil叶子节点为黑色,也在此场景的覆盖范围内)。
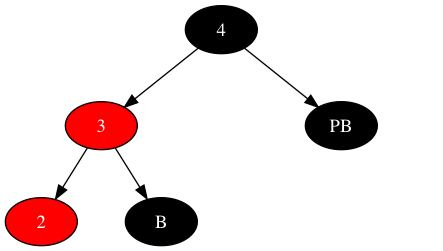
按照之前的思路,将左子树中其中一个红色节点挪到右子树,此时出问题了:若挪动新节点之父(红色节点3),节点B该如何放?若挪动新节点(红色节点2),其左右子树该如何放?挪动新节点,需要考虑其左右子树两棵树的移动,且最小子树场景扩展到了四层,而挪动新节点之父仅需要考虑一个子树的移动,所以优先考虑移动新节点之父。同时为新节点的兄弟(黑色节点B)找一个安身立命之所,可获得中间状态如下(新节点可能是双子节点,所以节点B只能随着上图中新节点之父移动):
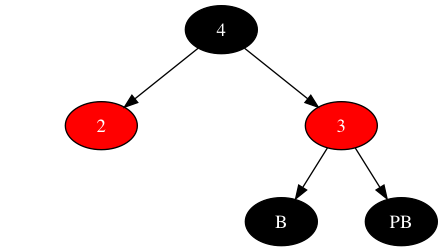
对3、4这两个数据对象重新排序,可以获得最终状态如下:
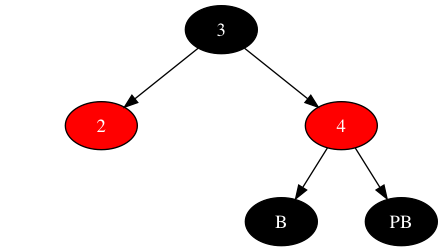
最终状态对比初始状态,若将初始状态上的三个节点(2、3、4)看做在一个圆周上,则恰似做了一次顺时针旋转:将新节点(2)挪到了新节点之父的位置,将新节点之父(3)挪到了子树根节点的位置,将子树根节点(4)挪到了新节点之父兄弟的位置;新节点的兄弟(B),就如同秒针一样,顺时针转动了两个节点,从新节点之父(3)转到新节点之父兄弟(PB)的位置。其中子树根节点保持颜色不变,其他节点颜色跳过子树根节点顺时针旋转。
此时还有一个遗留问题:节点B是否破坏了红黑树?
- 从颜色角度(是否违反红黑树规则),节点B与子树根节点依然保持着红-黑-红的结构,满足所有红黑树规则。
- 从数据角度(是否违反二叉树规则),节点B的数据对象必须小于其新父节点数据对象(原子树根节点数据对象),必然成立;节点B的数据对象必须大于新子树根节点数据对象(原B的父节点数据对象),此时限定了原节点B必须是右子。即调整前,新节点为左子天然满足情况,若新节点是右子,则必然违反二叉树规则。
继续分析新节点是右子树场景,如下:
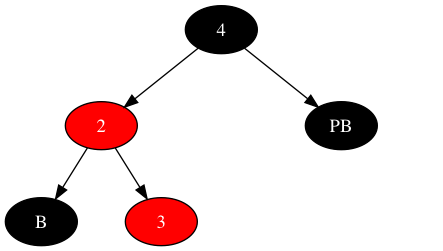
按照对上述遗留问题的分析,在三层最小子树场景下无法一次调整到位,不妨先尝试将左子树构建出左子红子右黑的场景。左子树的三层最小子树场景如下:
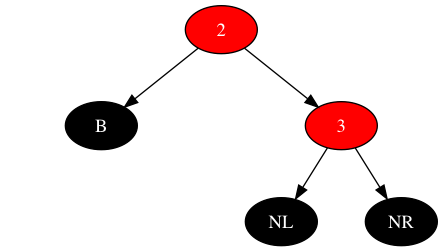
若将红色节点2挪到左子树,所需场景便可构建出来。此时的情况恰好与将左子树中红色的新节点之父挪到右子树相反,可以回顾下操纵子树进行顺时针旋转的场景,做一次逆时针旋转。逆时针旋转后场景如下:
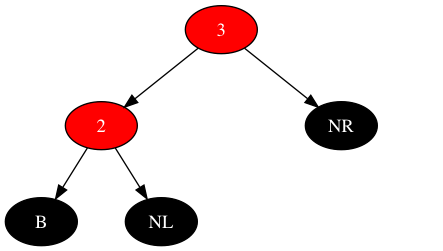
再观察完整的子树,如下:
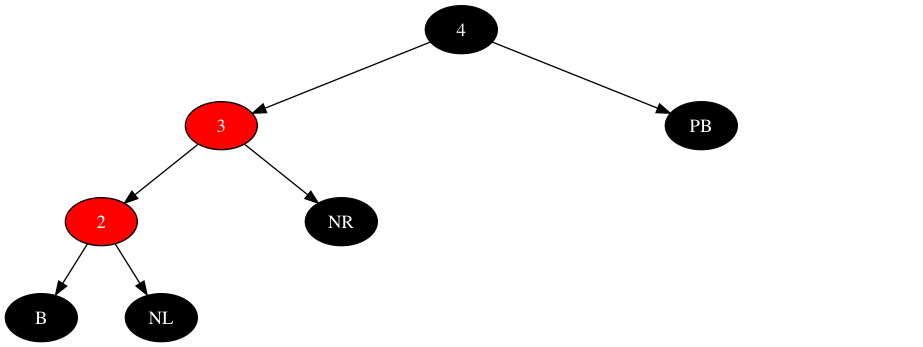
最后进行一次逆时针旋转,如下:
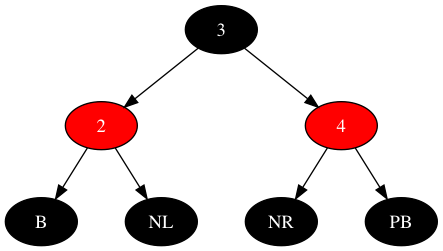
完善父为红色,父兄弟为黑色的场景,整个红黑树新增节点的情况便全部覆盖。
总结梳理
插入红色新节点的规则如下:
- 插入位置为根节点,标记为黑色
- 插入新节点之父为黑色,无需调整,已满足红黑树规则
- 插入新节点之父为红色,新节点之父兄弟为红色,标记祖父节点为红色,父与父兄弟为黑色,以祖父节点为新节点继续调整树
- 插入新节点之父为红色,新节点之父兄弟为黑色,对树进行旋转
红黑树旋转规则:
- 场景1:右父右祖,顺时针旋转
- 场景2:左父左祖,逆时针旋转
- 场景3:左父右祖,先逆时针旋转成右父右祖,再顺时针旋转
- 场景4:右父左祖,先顺时针旋转成左父左祖,再逆时针旋转
场景1、场景2,子与父、父与祖父关系一致,旋转过程看上去像往树的中心靠拢,可称为内旋; 场景3、场景4,子与父、父与祖父关系不同,首次旋转看上去像背离树的中心,可称为外旋。
RB-tree之删
参考ADT之删,删除的节点最终是删除单子节点或叶子节点。情况相对新增场景要复杂很多,节点的位置不一定是叶子节点,节点的颜色也不一定是红色。
分析删除动作,从二叉查找树的角度,销毁其数据对象;从红黑树的角度,销毁了一个颜色。销毁数据对象,ADT之删的场景已然调整满足,销毁一个颜色,那就不得了了。规则1、规则2、规则5肯定是满足的,对于规则3、规则4,删除的节点是红色还好,若是黑色,规则3和规则4必然被打破。这种情况下,直观分析可以有两种方案,来保证红黑树的平衡:
- 转移节点数据对象或移动节点颜色,直到待删除的数据对象是红色的单子节点或叶子节点,再删除;
- 删除节点,将节点颜色留给继承其位置的节点,继承的节点(Inherit Node,后简化为”I节点“)可能带有数据的节点,也可能是nil叶子节点,再从继承的节点上,平衡掉新增的颜色。
本文主要使用第2种方案(有篇文章是如此介绍,介绍方式略有不同,偷懒了)。
寻找稳定态
方案2删除节点后保证了树的平衡,但有新问题出现,继承的节点将包含两种颜色:”红+黑“+”黑+红“、”黑+黑“(由于规则3,不会出现”红+红“的场景)。以下便基于此三种场景进行分析:
- 根节点。根节点比较特殊,单独拿出优先分析。参见RB-tree之增中对于根节点的描述,刚好与新增节点中扩容的意义相反,每当有黑色需要在根节点平衡掉时,可以认为是树的减容,即逃生通道。
- 红+黑,由于红色节点不参与平衡,所以红+黑=黑,直接标记节点为黑即可
- 黑+红,同上,直接标记节点为黑即可
- 黑+黑,详细分析如下
需要消灭多出的一个黑色,那最好在I节点与I节点之父(IP)之间调入一个红色节点(R),如下所示:
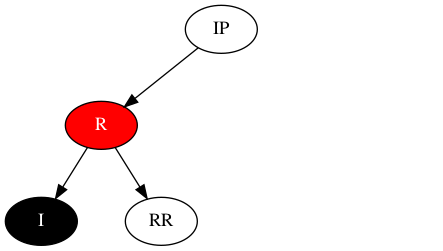
将I节点多出的黑色转移到R节点上,如下所示:
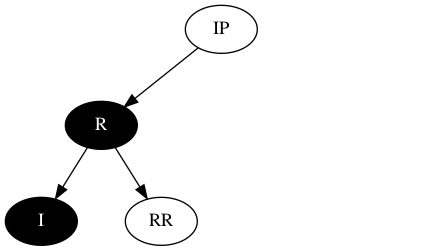
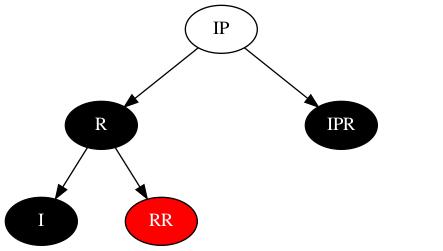
在RB-tree之增的场景下,调整树结构的方式是通过旋转,若此处的R节点通过旋转而来,则期望结构如下:
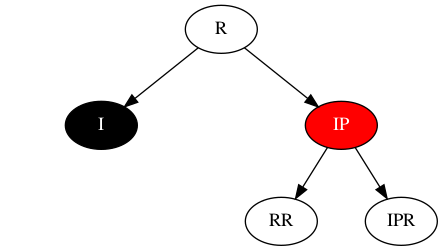
刷新旋转后结构为,如下:
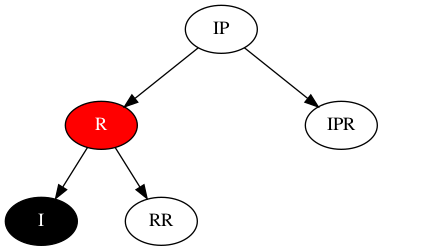
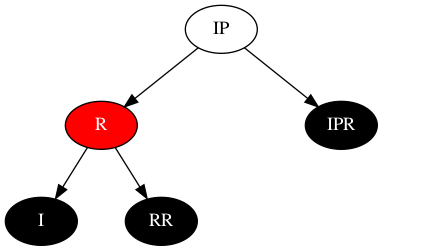
但此处不能抽调RR的颜色,否则将需要判断RR是否是黑色,且其子对象中是否包含红色节点,事情将变得更复杂。所以要求,RR节点也包含两种颜色,且其中一种是黑色。则只能是IP节点为黑色(下图所示),旋转前,IP先将黑色交给其子对象,即IP变为红色,RR、IPR变成两种颜色,其中一种为IP的黑色。RR在旋转后,同I节点一起交出一个黑色给R,达成单色;IPR只有在其颜色为红时,才能与多出的黑色达成单色,即黑色。因此需要的结构如下,即需要构建的稳定态:
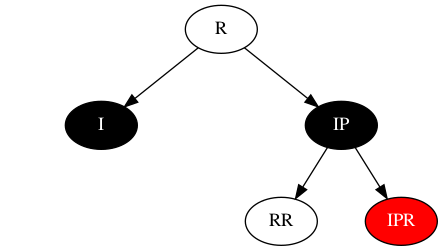
IP将黑色下沉给子节点后,逆时针旋转(其中I为”黑+黑“,RR多出一个黑色,IPR多出一个黑色与其本身的红色合并为黑色),结构如下:
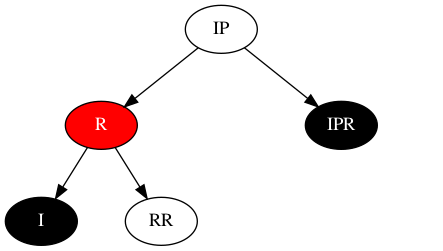
将I节点、RR节点多出的黑色转移到R节点上,最终结果如下所示:
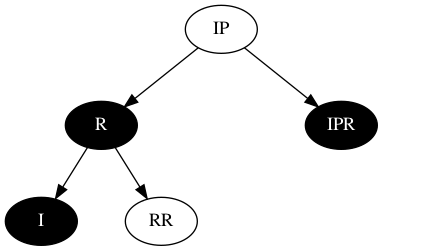
稳定态场景闭环
从以上的分析,当构建三层子树达成以下结构时,可通过旋转转换达成RB-tree的再次稳定,或进入根节点逃生通道。
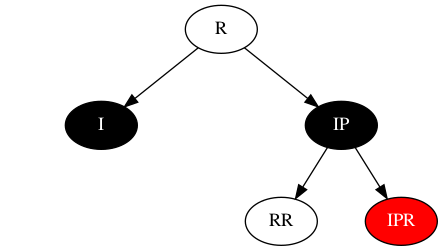
按以上结构,若要覆盖所有场景,那需要继续覆盖:
- IP = 红,RR=黑,IPR=黑
- IP = 黑,RR=?,IPR=黑
RR节点颜色未知,仅靠IP与IPR无法进行调整,则对RR节点做精确分析,整理覆盖场景如下:
- IP = 红,RR=黑,IPR=黑
- IP = 黑,RR=红,IPR=黑
- IP = 黑,RR=黑,IPR=黑
- IP = 黑,RR=?,IPR=红(上图)
场景1:IP = 红,RR=黑,IPR=黑
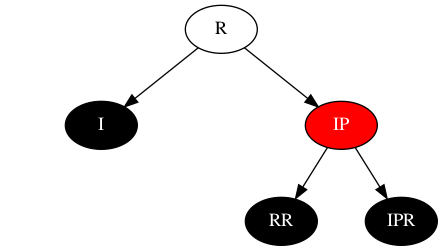
该场景与场景4相比,最直观的做法是先将RR和IPR的黑色转移到IP,IP变黑,RR、IPR变红,按照场景4运作最终的结果如下:
此时将面临新的问题,RR节点的子节点可能是红色,无法直接解决问题,且无法归类到其他场景,会导致算法膨胀,所以此方案先预留备用。
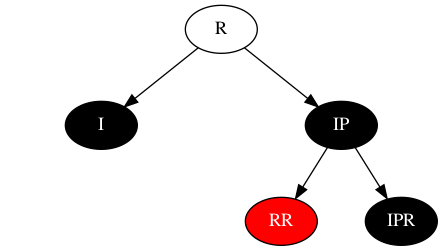
该场景最直观的、最诱人的动作,基于之前的分析,那便是将红色节点转移到与子树根节点之间,那不妨做一次逆时针旋转看看效果:
此时可以看到,I节点的兄弟节点为黑色的RR,场景1直接转换为了场景2、场景3或场景4,依然分析I节点。
场景2:IP = 黑,RR=红,IPR=黑
该场景与场景4相比,联想下RB-tree之增中的外旋场景(右父左祖),做一次外旋,便可得到场景4(其中RRR为RR的左叶子节点),旋转后的场景如下:
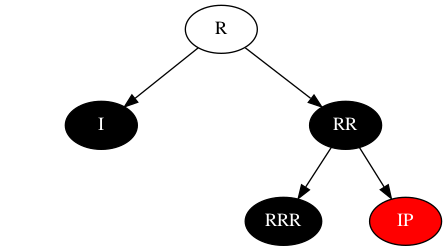
场景3:IP = 黑,RR=黑,IPR=黑
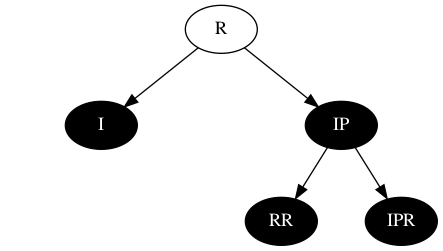
此时无红色节点可用,即无法考虑转换为场景4,唯一可考虑的便是从根节点逃脱。此时将I上”黑+黑“中不属于自己的黑色转移到R节点,那需要从R的另外一条分支上抽取一个黑色,可抽调IP上的黑色,IP变为红色,此时的结构如下:
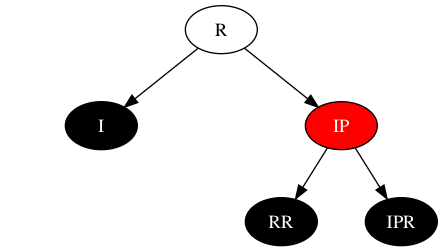
此时R节点包含两种颜色,原有的颜色+黑色,I已变为单纯的黑。继续以R节点为中心进行分析。
场景4:IP = 黑,RR=?,IPR=红
详见寻找稳定态。
总结梳理
删除节点的规则如下:
- 删除节点的颜色若转移到根节点,直接移除颜色
- 删除节点的颜色若转移到红色节点,直接标记节点颜色为黑
- 删除节点的颜色若转移到黑色节点,进行旋转变色
红黑树旋转变色规则:
- 兄弟节点为红,以兄弟节点做一次内旋,转换为其他三种场景中的一种
- 兄弟节点为黑,兄弟节点左子为红右子为黑,以兄弟节点左子做一次外旋,转换为兄弟节点为黑,兄弟节点左子为黑右子为红的场景
- 兄弟节点为黑,兄弟节点左子为黑右子为黑,提取自身多出的黑色与兄弟节点的黑色(兄弟节点变红),将父节点标记多一个黑色,继续以父节点进行分析
- 兄弟节点为黑,兄弟节点左子为黑右子为红,以兄弟节点做一次内旋,兄弟节点右子的红色与当前节点的黑色中和。
Author 朦呆农码
LastMod 2018-05-15